|
DE
SECTIO AUREA - IN GEOMETRIA
|
 Questa
è un'antica edizione degli Elementi di Euclide ed è qui che cominciamo a
sentire i primi odori della sezione aurea. La proposizione 11 del libro II
recita così: "Come dividere un segmento in modo che il rettangolo che ha
per lati l'intero segmento e la parte minore sia equivalente al quadrato che ha
per lato la parte maggiore", ovvero come trovare la Sezione Aurea di un
segmento, cioè la parte media proporzionale tra l'intero segmento e la parte
rimanente.
Questa
è un'antica edizione degli Elementi di Euclide ed è qui che cominciamo a
sentire i primi odori della sezione aurea. La proposizione 11 del libro II
recita così: "Come dividere un segmento in modo che il rettangolo che ha
per lati l'intero segmento e la parte minore sia equivalente al quadrato che ha
per lato la parte maggiore", ovvero come trovare la Sezione Aurea di un
segmento, cioè la parte media proporzionale tra l'intero segmento e la parte
rimanente.
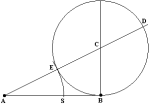 La
costruzione è tra le più classiche della Geometria: dato il segmento AB
tracciare il cerchio di pari diametro e tangente
ad esso in B, quindi la secante per A
passante per il centro C del cerchio.
La parte esterna della secante (AE)
è la sezione aurea del segmento, essendo la tangente (AB)
media proporzionale tra l'intera secante (AD)
e la sua parte esterna (AE), essendo ED
= AB e per alcune proprietà delle proporzioni:
La
costruzione è tra le più classiche della Geometria: dato il segmento AB
tracciare il cerchio di pari diametro e tangente
ad esso in B, quindi la secante per A
passante per il centro C del cerchio.
La parte esterna della secante (AE)
è la sezione aurea del segmento, essendo la tangente (AB)
media proporzionale tra l'intera secante (AD)
e la sua parte esterna (AE), essendo ED
= AB e per alcune proprietà delle proporzioni:
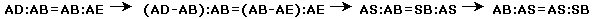
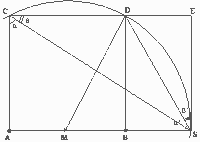 Volendo
invece trovare quel segmento di cui un dato segmento AB sia la Sezione Aurea, si procede nel modo seguente:
Volendo
invece trovare quel segmento di cui un dato segmento AB sia la Sezione Aurea, si procede nel modo seguente:
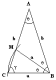
trovare il punto medio M del
segmento dato;
costruire il quadrato sul segmento dato; siano C e D gli altri due
vetrici;
centrato in M tracciare il
cerchio con raggio MC (=
MD), che interseca in S il
prolungamento di AB.
AS è il segmento cercato, di cui AB
è la Sezione Aurea.
Infatti i
triangoli CAS e SBD sono simili perché rettangoli e con gli angoli a ed a’ uguali (essendo uguali i loro complementari b e b’, angoli alla circonferenza che sottendono lo stesso
arco DS); quindi i cateti sono in
proporzione: 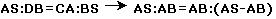
Ma
cosa ha di così importante questa sezione per meritarsi l'aggettivo "Aureo"?
Lo scopriremo attraverso le sue proprietà. Restando nella Geometria ne
ricaviamo immediatamente una: «Ogni segmento è sezione aurea della sua
somma con la sua sezione aurea»; ed in effetti questo è quanto sopra si è
dimostrato. Ne segue che: «Tolta la sezione aurea, la parte rimanente di un
segmento è la sezione aurea della sezione aurea del segmento». E’
come se la sezione aurea si autorigenerasse per sottrazione o addizione.
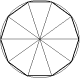
 Ma scopriamone altre caratteristiche. Sempre in
Geometria una delle più importanti caratteristiche della Sezione Aurea è la
seguente: "Se in un triangolo isoscele la base è la sezione aurea del lato,
allora l’angolo al vertice è un quinto dell’angolo piatto, ovvero la base
è il lato del decagono regolare inscritto nel cerchio che ha per raggio il lato".
Sorvoliamo sulle dimostrazioni (che sono abbastanza semplici e reperibili su
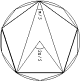
qualsiasi libro di geometria) e proseguiamo: collegando alternativamente i
vertici del decagono si ottiene il pentagono regolare inscritto nel cerchio;
tracciatone due diagonali dallo stesso vertice, essendo l’angolo alla
circonferenza metà di quello al centro di 2p/5,
si ripropone con il lato opposto al vertice il triangolo isoscele con angolo al
vertice di p/5;
ne segue che in un pentagono regolare il lato è la sezione aurea della
diagonale. Si può altresì dimostrare che le diagonali si intersecano secondo
le loro sezioni auree. Per questi motivi alla stella a cinque punte disegnata
dalle diagonali di un pentagono venivano riconosciuti poteri magici.
Ma scopriamone altre caratteristiche. Sempre in
Geometria una delle più importanti caratteristiche della Sezione Aurea è la
seguente: "Se in un triangolo isoscele la base è la sezione aurea del lato,
allora l’angolo al vertice è un quinto dell’angolo piatto, ovvero la base
è il lato del decagono regolare inscritto nel cerchio che ha per raggio il lato".
Sorvoliamo sulle dimostrazioni (che sono abbastanza semplici e reperibili su
qualsiasi libro di geometria) e proseguiamo: collegando alternativamente i
vertici del decagono si ottiene il pentagono regolare inscritto nel cerchio;
tracciatone due diagonali dallo stesso vertice, essendo l’angolo alla
circonferenza metà di quello al centro di 2p/5,
si ripropone con il lato opposto al vertice il triangolo isoscele con angolo al
vertice di p/5;
ne segue che in un pentagono regolare il lato è la sezione aurea della
diagonale. Si può altresì dimostrare che le diagonali si intersecano secondo
le loro sezioni auree. Per questi motivi alla stella a cinque punte disegnata
dalle diagonali di un pentagono venivano riconosciuti poteri magici.
Consideriamo ora il triangolo isoscele con
angolo al vertice di p/5:
un triangolo di tal genere viene definito come triangolo aureo poiché
tracciando la bisettrice di un angolo alla base questa interseca il lato opposto
in un punto che lo divide nel Rapporto Aureo e si determina così un secondo
triangolo simile al primo; con la stessa operazione su questo secondo si può
determinare un terzo triangolo simile al secondo e così via ottenendo triangoli
sempre più piccoli ma sempre simili tra loro. In modo analogo prolungando la
base per un tratto uguale al lato e congiungendo l’estremo con il vecchio
vertice, si ottiene un nuovo triangolo maggiore del primo e ad esso simile, sul
quale si può operare la stessa costruzione per ottenere un triangolo ancora più
grande ma ancora simile ai precedenti e così via ottenendo triangoli sempre più
grandi.
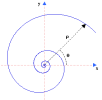 I punti "aurei", cioè i punti di intersezione delle
bisettrici dell'angolo di base con il lato opposto, si trovano tutti lungo una
curva denominata spirale logaritmica. La stessa cosa accade con un rettangolo
aureo che, ricordiamo, è tale se il lato minore è sezione aurea di quello
maggiore. La spirale logaritmica è
una delle curve più famose e fu forse considerata già dagli antichi egizi; lo
fu certamente dagli antichi greci, ma occorre attendere il 17° secolo per una
prima rigorosa definizione ed un approfondito studio delle sue proprietà. Si
deve a Descartes, nel 1638, una prima definizione. Qualche anno dopo Torricelli
la studiò scoprendone una delle più sorprendenti caratteristiche: sebbene la
curva compia infinite evoluzioni intorno al suo polo d’origine, la lunghezza
dell’arco di curva da ogni punto fino all’origine è finita. Ma più di
tutti l’ammirò Jacob Bernoulli definendola "Spira mirabilis" e che
se la fece scolpire sulla sua tomba insieme alla frase "Eadem mutata
resurgo". Si nota che la curva esegue infinite evoluzioni intorno al suo
polo sia verso l'infinitamente grande che verso l'infinitamente piccolo.
I punti "aurei", cioè i punti di intersezione delle
bisettrici dell'angolo di base con il lato opposto, si trovano tutti lungo una
curva denominata spirale logaritmica. La stessa cosa accade con un rettangolo
aureo che, ricordiamo, è tale se il lato minore è sezione aurea di quello
maggiore. La spirale logaritmica è
una delle curve più famose e fu forse considerata già dagli antichi egizi; lo
fu certamente dagli antichi greci, ma occorre attendere il 17° secolo per una
prima rigorosa definizione ed un approfondito studio delle sue proprietà. Si
deve a Descartes, nel 1638, una prima definizione. Qualche anno dopo Torricelli
la studiò scoprendone una delle più sorprendenti caratteristiche: sebbene la
curva compia infinite evoluzioni intorno al suo polo d’origine, la lunghezza
dell’arco di curva da ogni punto fino all’origine è finita. Ma più di
tutti l’ammirò Jacob Bernoulli definendola "Spira mirabilis" e che
se la fece scolpire sulla sua tomba insieme alla frase "Eadem mutata
resurgo". Si nota che la curva esegue infinite evoluzioni intorno al suo
polo sia verso l'infinitamente grande che verso l'infinitamente piccolo.
L'architecture bureau projet - Curiosité est/et
intelligence
 Questa
è un'antica edizione degli Elementi di Euclide ed è qui che cominciamo a
sentire i primi odori della sezione aurea. La proposizione 11 del libro II
recita così: "Come dividere un segmento in modo che il rettangolo che ha
per lati l'intero segmento e la parte minore sia equivalente al quadrato che ha
per lato la parte maggiore", ovvero come trovare la Sezione Aurea di un
segmento, cioè la parte media proporzionale tra l'intero segmento e la parte
rimanente.
Questa
è un'antica edizione degli Elementi di Euclide ed è qui che cominciamo a
sentire i primi odori della sezione aurea. La proposizione 11 del libro II
recita così: "Come dividere un segmento in modo che il rettangolo che ha
per lati l'intero segmento e la parte minore sia equivalente al quadrato che ha
per lato la parte maggiore", ovvero come trovare la Sezione Aurea di un
segmento, cioè la parte media proporzionale tra l'intero segmento e la parte
rimanente.  La
costruzione è tra le più classiche della Geometria: dato il segmento AB
tracciare il cerchio di pari diametro e
La
costruzione è tra le più classiche della Geometria: dato il segmento AB
tracciare il cerchio di pari diametro e 


 Ma scopriamone altre caratteristiche. Sempre in
Geometria una delle più importanti caratteristiche della Sezione Aurea è la
seguente: "Se in un triangolo isoscele la base è la sezione aurea del lato,
allora l’angolo al vertice è un quinto dell’angolo piatto, ovvero la base
è il lato del decagono regolare inscritto nel cerchio che ha per raggio il lato".
Sorvoliamo sulle dimostrazioni (che sono abbastanza semplici e reperibili su
qualsiasi libro di geometria) e proseguiamo: collegando alternativamente i
vertici del decagono si ottiene il pentagono regolare inscritto nel cerchio;
tracciatone due diagonali dallo stesso vertice, essendo l’angolo alla
circonferenza metà di quello al centro di 2p/5,
si ripropone con il lato opposto al vertice il triangolo isoscele con angolo al
vertice di p/5;
ne segue che in un pentagono regolare il lato è la sezione aurea della
diagonale. Si può altresì dimostrare che le diagonali si intersecano secondo
le loro sezioni auree. Per questi motivi alla stella a cinque punte disegnata
dalle diagonali di un pentagono venivano riconosciuti poteri magici.
Ma scopriamone altre caratteristiche. Sempre in
Geometria una delle più importanti caratteristiche della Sezione Aurea è la
seguente: "Se in un triangolo isoscele la base è la sezione aurea del lato,
allora l’angolo al vertice è un quinto dell’angolo piatto, ovvero la base
è il lato del decagono regolare inscritto nel cerchio che ha per raggio il lato".
Sorvoliamo sulle dimostrazioni (che sono abbastanza semplici e reperibili su
qualsiasi libro di geometria) e proseguiamo: collegando alternativamente i
vertici del decagono si ottiene il pentagono regolare inscritto nel cerchio;
tracciatone due diagonali dallo stesso vertice, essendo l’angolo alla
circonferenza metà di quello al centro di 2p/5,
si ripropone con il lato opposto al vertice il triangolo isoscele con angolo al
vertice di p/5;
ne segue che in un pentagono regolare il lato è la sezione aurea della
diagonale. Si può altresì dimostrare che le diagonali si intersecano secondo
le loro sezioni auree. Per questi motivi alla stella a cinque punte disegnata
dalle diagonali di un pentagono venivano riconosciuti poteri magici. I punti "aurei", cioè i punti di intersezione delle
bisettrici dell'angolo di base con il lato opposto, si trovano tutti lungo una
curva denominata spirale logaritmica. La stessa cosa accade con un rettangolo
aureo che, ricordiamo, è tale se il lato minore è sezione aurea di quello
maggiore. La spirale logaritmica è
una delle curve più famose e fu forse considerata già dagli antichi egizi; lo
fu certamente dagli antichi greci, ma occorre attendere il 17° secolo per una
prima rigorosa definizione ed un approfondito studio delle sue proprietà. Si
deve a Descartes, nel 1638, una prima definizione. Qualche anno dopo Torricelli
la studiò scoprendone una delle più sorprendenti caratteristiche: sebbene la
curva compia infinite evoluzioni intorno al suo polo d’origine, la lunghezza
dell’arco di curva da ogni punto fino all’origine è finita. Ma più di
tutti l’ammirò Jacob Bernoulli definendola "Spira mirabilis" e che
se la fece scolpire sulla sua tomba insieme alla frase "Eadem mutata
resurgo". Si nota che la curva esegue infinite evoluzioni intorno al suo
polo sia verso l'infinitamente grande che verso l'infinitamente piccolo.
I punti "aurei", cioè i punti di intersezione delle
bisettrici dell'angolo di base con il lato opposto, si trovano tutti lungo una
curva denominata spirale logaritmica. La stessa cosa accade con un rettangolo
aureo che, ricordiamo, è tale se il lato minore è sezione aurea di quello
maggiore. La spirale logaritmica è
una delle curve più famose e fu forse considerata già dagli antichi egizi; lo
fu certamente dagli antichi greci, ma occorre attendere il 17° secolo per una
prima rigorosa definizione ed un approfondito studio delle sue proprietà. Si
deve a Descartes, nel 1638, una prima definizione. Qualche anno dopo Torricelli
la studiò scoprendone una delle più sorprendenti caratteristiche: sebbene la
curva compia infinite evoluzioni intorno al suo polo d’origine, la lunghezza
dell’arco di curva da ogni punto fino all’origine è finita. Ma più di
tutti l’ammirò Jacob Bernoulli definendola "Spira mirabilis" e che
se la fece scolpire sulla sua tomba insieme alla frase "Eadem mutata
resurgo". Si nota che la curva esegue infinite evoluzioni intorno al suo
polo sia verso l'infinitamente grande che verso l'infinitamente piccolo.