I matematici ritengono che,
con tutta probabilità, il mondo dei numeri esisteva già prima che l'uomo lo
scoprisse. Questa convinzione è talmente radicata da aver generato, in alcuni,
il pensiero che lo stesso Creatore abbia posto la matematica (e quindi i numeri)
alla base tutta la Sua mirabile opera.
Infatti, sembra che dietro l'idea di
armonia e di perfezione, si celi un numero il cui valore non è esprimibile in
cifre decimali se non in forma approssimata: 1,6180... Si tratta di un numero
irrazionale ed è, con "pi greco", il più celebre fra i numeri di
questa specie. Si deve al matematico americano Mark Barr la proposta, poi
universalmente accetta, di indicare questo numero con la lettera greca "phi"
in onore del più grande artista del mondo classico, Fidia.
Che cosa hanno in comune la
disposizione dei petali di rosa e dei semi nelle mele o nel girasole, la forma a spirale di
alcune conchiglie, gli ammassi di galassie, un quadro come il "Sacramento
dell'Ultima Cena" di Salvador Dalì, i progetti di Le Corbusier (e, per
alcuni, il Partenone o la grande piramide di Giza), e la successione di
Fibonacci (1, 1, 2, 3, 5, 8, 13, 21, 34, 55..., in cui ogni numero è la somma
dei due che lo precedono)?
 Per quanto strano possa sembrare, in queste realtà così
disparate si nasconde (o è stato cercato) un numero particolare, una
proporzione geometrica scoperta dai pitagorici, definita da Euclide e chiamata
da Pacioli “divina proportione”, da Keplero “sectio
divina”, da Leonardo e fino ai giorni nostri “sectio
aurea”, sezione aurea.
Per quanto strano possa sembrare, in queste realtà così
disparate si nasconde (o è stato cercato) un numero particolare, una
proporzione geometrica scoperta dai pitagorici, definita da Euclide e chiamata
da Pacioli “divina proportione”, da Keplero “sectio
divina”, da Leonardo e fino ai giorni nostri “sectio
aurea”, sezione aurea.
«Phi» tende a mostrarsi nei
luoghi più impensati, e ha affascinato matematici, artisti, musicisti, storici,
architetti, psicologi, perfino mistici e cultori dell'esoterico.
Avete mai interrogato i
petali della margherita intorno alla fatale domanda «m’ama, non m’ama»? La
maggior parte delle margherite di campo ha tredici, ventuno o trentaquattro
petali, numeri di Fibonacci (si noti che due margherite su tre hanno un numero
dispari di petali; dunque, cominciando con m’ama, il buon esito è quasi
garantito).
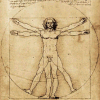 Marcus Vitruvius Pollio (70-25 a.C.), nel «De Architectura» Libro III,1,3
dice: «Item corporis centrum medium naturaliter est umbilicus. Namque si homo
conlocatus fuerit supinus manibus et pedibus pansis circinique conlocatum
centrum in umbilico eius, circumagendo rotundationem utrarumque manuum et pedum
digiti linea tangentur». (Sui
significati ermetici nell’Homo ad circulum di Leonardo, consiglio una visita
al sito Airesis)
Marcus Vitruvius Pollio (70-25 a.C.), nel «De Architectura» Libro III,1,3
dice: «Item corporis centrum medium naturaliter est umbilicus. Namque si homo
conlocatus fuerit supinus manibus et pedibus pansis circinique conlocatum
centrum in umbilico eius, circumagendo rotundationem utrarumque manuum et pedum
digiti linea tangentur». (Sui
significati ermetici nell’Homo ad circulum di Leonardo, consiglio una visita
al sito Airesis)
Alcuni sostenitori della tesi
secondo la quale il «numero d’oro» o «costante di Fidia» sia in ogni cosa
bella, proporzionata ed armonica vedono rapporti aurei in gran parte del corpo
umano: viso, mani e relative falangi delle dita, braccia, gambe, altezza totale. Ad
esempio, se la tua altezza è 175 cm, perché tu possa considerarti un perfetto
esemplare "aureo" il tuo ombellico deve trovarsi a circa 108,15 cm da terra, deve
cioè essere vera la relazione:
|
H/h1= |
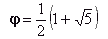
|
=1,61803398…... |
(dove H è l’altezza totale ed h1
è l’altezza alla quale si trova l’ombellico). |
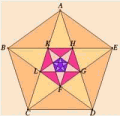 I
pitagorici, studiando le figure geometriche e in particolare il pentagono
regolare, notarono che unendo con un segmento i vertici in tutti i modi possibili, si ottiene
un pentagramma (la stella a cinque punte) che, a sua volta, contiene un pentagono regolare nella sua parte
interna. Il procedimento può essere reiterato all'infinito: da un pentagono si
ottiene un pentagramma che contiene un pentagono che può essere suddiviso in un
pentagramma che .... ecc.
I
pitagorici, studiando le figure geometriche e in particolare il pentagono
regolare, notarono che unendo con un segmento i vertici in tutti i modi possibili, si ottiene
un pentagramma (la stella a cinque punte) che, a sua volta, contiene un pentagono regolare nella sua parte
interna. Il procedimento può essere reiterato all'infinito: da un pentagono si
ottiene un pentagramma che contiene un pentagono che può essere suddiviso in un
pentagramma che .... ecc.
E'
facilmente dimostrabile come le coppie di segmenti AC e CD, CD e CL, CL e LF, sono
in rapporto aureo. Ma bisognerà aspettare più di due secoli e cioè
Euclide e i suoi Elementi per trovare una vera e propria definizione di rapporto
aureo e per vederlo applicato esplicitamente. Euclide se ne serve per costruire
il pentagono regolare (ancora il pentagono...), l'icosaedro (un solido composto
da venti triangoli equilateri) e il dodecaedro (un solido composto da dodici
pentagoni regolari). Questi ultimi, insieme con il cubo, il tetraedro e
l'ottaedro (un solido composto da otto triangoli equilateri), rappresentano i
famosi solidi platonici.
 Trascorreranno
circa 1500 anni prima di risentir parlare di rapporti aurei con la celebre
successione fibonacciana e, a partire da questa, è un autentico tripudio: viene ripetuta come un ritornello in tutte le salse ed in tutti i secoli a
venire fino ai giorni nostri. Se ne occuparono una moltitudine di studiosi e
matematici tra cui spicca Piero della Francesca, poi il frate
Luca Pacioli ne immortalò i concetti nel "De Divina Proportione" con
disegni e illustrazioni dello stesso Leonardo, seguì Keplero che la definì
"un autentico gioiello"; poi numerosi musicisti tra il XIX e il XX
secolo tra cui emergono Debussy e Bartòk, infine Le Corbusier con il suo "Modulor"
ne introdusse l’applicazione nell’architettura moderna.
Trascorreranno
circa 1500 anni prima di risentir parlare di rapporti aurei con la celebre
successione fibonacciana e, a partire da questa, è un autentico tripudio: viene ripetuta come un ritornello in tutte le salse ed in tutti i secoli a
venire fino ai giorni nostri. Se ne occuparono una moltitudine di studiosi e
matematici tra cui spicca Piero della Francesca, poi il frate
Luca Pacioli ne immortalò i concetti nel "De Divina Proportione" con
disegni e illustrazioni dello stesso Leonardo, seguì Keplero che la definì
"un autentico gioiello"; poi numerosi musicisti tra il XIX e il XX
secolo tra cui emergono Debussy e Bartòk, infine Le Corbusier con il suo "Modulor"
ne introdusse l’applicazione nell’architettura moderna.
La
marcia trionfale del "numero d'oro" ha fatto la sua
irruzione anche nella popular musik, in particolare nel cosiddetto rock
progressivo. Qui i Genesis (una rock band inglese attiva dal 1969 al 1997) hanno
toccato l'apice per ciò che riguarda gli aspetti mistico-esoterici della «sectio
aurea», e più precisamente della serie di Fibonacci: l’architettura
armonico-temporale di vari brani musicali si fonda proprio su quella
"magica" sequenza che in Firth of Fifth viene esaltata e
ripetutamente proposta. Se non ricordi questo celeberrimo
"pezzo" ti propongo di riascoltarlo cliccando
qui (è una versione tradotta in un midi con tutte le limitazioni
di questo tipo di file; per apprezzarlo meglio ti suggerisco di scaricare il
file mp3
zippato però pesa 9 Mb).
Se ti interessa un'ampia dissertazione sulle
incursioni della sezione aurea in ambito musicale, allora non puoi fare a meno
di leggere questo studio di Gaudenzio
Temporelli (è suddiviso in due parti: la prima dedicata alla musica classica,
la seconda ai Genesis). Il saggio è alquanto lunghetto e se te lo vuoi godere
con calma, scaricalo cliccando qui.
A
voler seguire i fautori del "numero d'oro" in ogni cosa, si inciampa
nella sezione aurea ad ogni passo. Si va dalla disposizione delle foglie sui
rami degli alberi, al macrocosmo dell'universo intero per il sol fatto che molte
galassie hanno un aspetto spiraliforme (e sì, anche la spirale -quella
logaritmica- ha da dire la sua). Quello che è certo è il fascino indiscutibile
che ha l'argomento ma, a parer mio, solo sotto l'aspetto di speculazione
matematica e se elidiamo tutta la zavorra mistico-esoterica.
A
questo punto, se ancora sei interessato alla "divina proportione", e a
come si calcolano i rapporti aurei, beh, questo è tutto quanto bisogna
sapere sulla geometria e sulla
matematica della sezione aurea.
Se,
invece, vuoi approfondire in modo specifico l'argomento, allora questa è una
bibliografia essenziale.
 Per quanto strano possa sembrare, in queste realtà così
disparate si nasconde (o è stato cercato) un numero particolare, una
proporzione geometrica scoperta dai pitagorici, definita da Euclide e chiamata
da Pacioli “divina proportione”, da Keplero “sectio
divina”, da Leonardo e fino ai giorni nostri “sectio
aurea”, sezione aurea.
Per quanto strano possa sembrare, in queste realtà così
disparate si nasconde (o è stato cercato) un numero particolare, una
proporzione geometrica scoperta dai pitagorici, definita da Euclide e chiamata
da Pacioli “divina proportione”, da Keplero “sectio
divina”, da Leonardo e fino ai giorni nostri “sectio
aurea”, sezione aurea. Marcus Vitruvius Pollio (70-25 a.C.), nel «De Architectura» Libro III,1,3
dice: «Item corporis centrum medium naturaliter est umbilicus. Namque si homo
conlocatus fuerit supinus manibus et pedibus pansis circinique conlocatum
centrum in umbilico eius, circumagendo rotundationem utrarumque manuum et pedum
digiti linea tangentur».
Marcus Vitruvius Pollio (70-25 a.C.), nel «De Architectura» Libro III,1,3
dice: «Item corporis centrum medium naturaliter est umbilicus. Namque si homo
conlocatus fuerit supinus manibus et pedibus pansis circinique conlocatum
centrum in umbilico eius, circumagendo rotundationem utrarumque manuum et pedum
digiti linea tangentur».  I
pitagorici, studiando le figure geometriche e in particolare il pentagono
regolare, notarono che unendo con un segmento i vertici in tutti i modi possibili, si ottiene
un pentagramma (la stella a cinque punte) che, a sua volta, contiene un pentagono regolare nella sua parte
interna. Il procedimento può essere reiterato all'infinito: da un pentagono si
ottiene un pentagramma che contiene un pentagono che può essere suddiviso in un
pentagramma che .... ecc.
I
pitagorici, studiando le figure geometriche e in particolare il pentagono
regolare, notarono che unendo con un segmento i vertici in tutti i modi possibili, si ottiene
un pentagramma (la stella a cinque punte) che, a sua volta, contiene un pentagono regolare nella sua parte
interna. Il procedimento può essere reiterato all'infinito: da un pentagono si
ottiene un pentagramma che contiene un pentagono che può essere suddiviso in un
pentagramma che .... ecc. Trascorreranno
circa 1500 anni prima di risentir parlare di rapporti aurei con la celebre
successione fibonacciana e, a partire da questa, è un autentico tripudio: viene ripetuta come un ritornello in tutte le salse ed in tutti i secoli a
venire fino ai giorni nostri. Se ne occuparono una moltitudine di studiosi e
matematici tra cui spicca Piero della Francesca, poi il frate
Luca Pacioli ne immortalò i concetti nel "De Divina Proportione" con
disegni e illustrazioni dello stesso Leonardo, seguì Keplero che la definì
"un autentico gioiello"; poi numerosi musicisti tra il XIX e il XX
secolo tra cui emergono Debussy e Bartòk, infine Le Corbusier con il suo "Modulor"
ne introdusse l’applicazione nell’architettura moderna.
Trascorreranno
circa 1500 anni prima di risentir parlare di rapporti aurei con la celebre
successione fibonacciana e, a partire da questa, è un autentico tripudio: viene ripetuta come un ritornello in tutte le salse ed in tutti i secoli a
venire fino ai giorni nostri. Se ne occuparono una moltitudine di studiosi e
matematici tra cui spicca Piero della Francesca, poi il frate
Luca Pacioli ne immortalò i concetti nel "De Divina Proportione" con
disegni e illustrazioni dello stesso Leonardo, seguì Keplero che la definì
"un autentico gioiello"; poi numerosi musicisti tra il XIX e il XX
secolo tra cui emergono Debussy e Bartòk, infine Le Corbusier con il suo "Modulor"
ne introdusse l’applicazione nell’architettura moderna.